Insights from a Broken Calculator

Declaring the end from the beginning, and from ancient times things that are not yet done; saying: ‘My counsel shall stand, and all My pleasure will I do’

(Isaiah 46:10)

In elementary school we learned about numbers as if they were only for counting and calculating, skipping right over all the beauty of numbers and their meaning. So I was happy to have this “Calculator Puzzle” brought to my attention via a Twitter post. Not just for the mental exercise, but for the insights it brought about different parts of math (calculation, algebra, and geometry) to name a few, and about how my mind progresses from problem to solution. Definitely not by a straight line. But also not by a random walk.

Spolier Alert:
If you want to try to solve the problems yourself, do NOT read this post, nor my replies on the Twitter thread!

That said, here was my thought process:

Background

calculator is not working properly. Only the add and reciprocal buttons work, as well as the numbers 0-9.

Well that was interesting. Reciprocal is not a key that I often use on a calculator.

Question 1

Can you work out how to halve any number?

I admit, my first reaction, and the one I went with, was to try a specific example first. And, as above in Isaiah, to “declare the end from the beginning”.

Say, half of 5. That would be 5/2.

How could I get from “5” and “half” to 5/2, with only “+” and “1/x”?

Impressed by the unusual button — reciprocal — I immediately asked: could I get 2/5?

Well, yes. 1/5 + 1/5 is 2/5.

That was it: 5, 1/x, +, 5, 1/x, = would give 2/5. Another press on 1/x would give 5/2. Q.E.D.

Insight 1a*

Better than solving the problem, though, is that as an electrical engineer, I felt a sense of “coming home”. I hadn’t seen it at first, but this was “reciprocal of the sum of the reciprocals”. Well known as the resistance of a set of resistors in parallel. So it would certainly work for every case, because two equal resistors is two equal paths instead of one, offering half the resistance. Whether you feel that math or electricity is the original depends on whether you’re a mathematician or an engineer.

* Where’s 1b?? You’ll have to wait for that. I did.

Question 2

Now the subtract button has started working.

I think this means I can now square any number – can you work out how?

Here, I rushed ahead too quickly to generalize. I offered a solution where squaring is a special case of multiplication. The original questioner gently encouraged me to try again without repeated addition.

Back to my specific example. 5. 5 squared is 25. No way I would get directly to 25, but now that I was friends with that reciprocal button, I sought 1/25.

After a few minutes of that, I realized that I would have to use the “-” button. Surely it was working (in the problem) for a reason.

1/25 is pretty small. I would get it by subtracting fractions (which I could generate with the 1/x button). But I couldn’t think of any fractions to subtract, certainly not with a numerator of 1, that would yield 1/25. I did realize that fractions with denominators close to each other would yield significantly smaller fractions. How about 1/4 – 1/5 = 1/20. OK, 1/20 was not 1/25, but maybe I could fix it up. 1/20 would yield 20 (after pressing 1/x). Then simple enough to add 5 and get to 25.

5 squared = 5 + 1 / (1/4 – 1/5).

I generalized: n^2 = n + 1 / (1/(n-1) – 1/n)

Why would it work in general? Algebra:

n + 1 / ( (n – (n-1)) / (n(n-1))) = n + 1 / 1 / (n(n-1)) = n + n(n-1) = n + n^2 – n = n^2.

Q.E.D. again.

Insight 2

Why is 1/4 – 1/5 = 1/20? What’s special there? Suddenly, though I had never seen it written down, I thought: “Consecutive integers are relatively prime.” Then I looked that up to be sure. I read some proof discussions, and then left off that to continue the problem.

Question 3

Now, I think I can also calculate the product of any number. How?

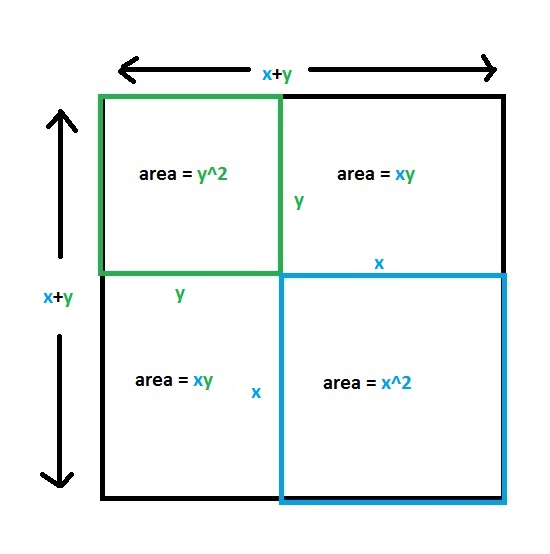
Here, I was onto the power of algebra to solve problems “automatically”. Instead of one number n, I would have two numbers x and y. I asked myself what product expressions involving x and y I was familiar with. The product (x+y)(x-y) came to mind. In high school it always seemed nice because it produced a sum of squares “cleanly” with no annoying middle term in xy. But here, I realized, “xy” was just what I was looking for. So the product would be the “messier” one: (x+y)(x+y). Which, by the way, is (x+y)^2. Aha! Is this is why the problem author tried to take me by the hand from square to product?

Anyway, (x+y)(x+y) = x^2 + 2xy + y^2. That could be solved for xy:

xy = ((x+y)(x+y)-(x^2 + y^2))/2.

Insight 3

I like geometrical interpretations more than, or at least in addition to, purely algebraic interpretations. Even if algebra works, I feel better seeing a picture too. So I went back and asked myself what picture matched that equation. Here it is (freehand drawing):

Insight 1b

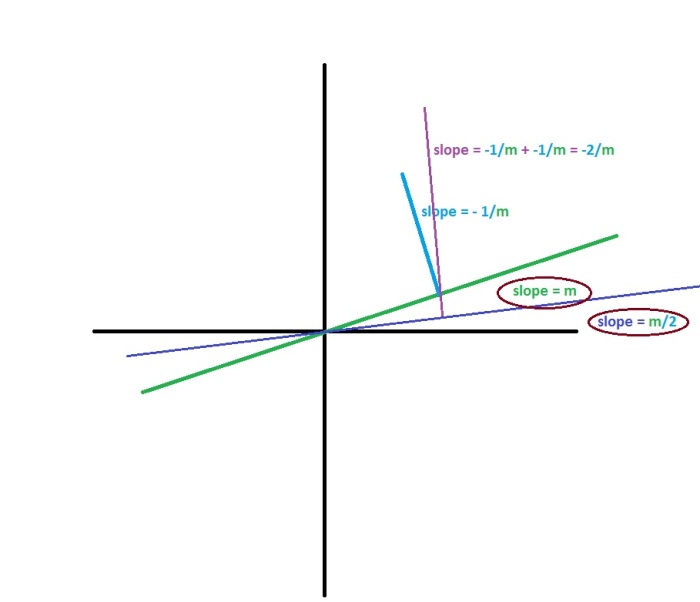
Now, even though I had solved question 1 without any algebraic symbols, I challenged myself to find a geometric interpretation for the reciprocal of the sum of the reciprocals, with two equal numbers yielding a half.

One geometric interpretation of reciprocal is the (negative of the) slope of the perpendicular. With that in mind, the picture came pretty quickly:

Question 4

Are there any other operations I can do with only add, subtract and reciprocal?

I left this for when I find more time. Or maybe a reader would like to offer some thoughts? Not just the “answers”, but your thought process, and any insights that come up for you!